Magnetic Field Vectors and Components
The magnetic field at any point in space is a vector quantity. This means there is a direction associated with the field as well as a field strength. Consider the arrow below:

The direction of the arrow can be thought of as the direction of the magnetic field. The length of the arrow can be thought of as the strength of the field, i.e. the longer the arrow, the stronger the field. Call this length B.
If I place set of axes on the arrow I can divide the field into two components of the field, namely the x component and the y component. Call these lengths Bx and By.
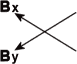
I can now describe the length of the arrow, or the strength of the magnetic field, in terms of the x and y components. Using the Pythagorean Theorem:
![]()
Now imagine that there exists a third direction, so that the arrow, B can be pointing out of (or into) the plane of the page. There is now a third component, namely Bz, which in our example is the length of the component stretching from the page outward to the tip of the arrow.
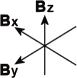
By exactly the same mathematics, I can now describe B as:
![]()
The value B, is the strength of the magnetic field. Bx, By, and Bz are the three components measured by a three axis teslameter (gaussmeter). A single axis measuring device will change its reading depending on which way the sensitive axis is oriented with respect to the direction of the magnetic field. To obtain a complete representation of magnetic field at any point in space, one needs not only the value of B, but the direction, which can be expressed as the three components, Bx, By and Bz.
Some magnetic field sensors measure only one component of the magnetic field (Fluxgates and Hall effect instruments). These are referred to as single axis devices.
Other instruments measure only the total field amplitude (NMR, ESR). This is the quantity B above.
It is possible to combine three axis sensors to give three field measurements in a single probe package. These are referred to as three-axis devices.
